Stabilizer codes#
We now have all the ingredients to define stabilizer codes. First note that to define a error-correcting code we need four ingredients
- Encoding: A method to encode each message into a codewords. For quantum codes, we need to map each basis element of the message space to a basis element of the codespace.
- Syndrome measurements: A method to do syndrome measurements on the corrupted codewords, to extract information about the error.
- Decoding: A method to transfrom the corrected codewords back into a message.
- Logical gates: Methods to implement logical gates directly on an encoded qubit.
Stabilizer codes are defined with respect to a stabilizer group $S$. We label the stabilizer code based on $S$ as $C(S)$. Then, the ingredients for $C(S)$ are
- Encoding: The simultaneous stabilizer states of the stabilizer group $S$ define the basis elements of the codespace. An encoding circuit can be systematically constructed using the generators of $S$; a procedure we will show later.
- Syndrome measurements: All generators of $S$ are measured one by one. The results of the measurement indicate which error has occured.
- Decoding: Decoding is also based on $S$.
- Logical gates: These can also be constructed from $S$.
Repetition code for bit-flips#
Let's see how all this applies to the repetition code. The repetition code is based on the group $S$ generated by $P_1 = Z \otimes Z \otimes I$ and $P_2 = Z \otimes I \otimes Z$.
Encoding: We saw in stabilizer groups that this group simultaneously stabilizes the states $\set{\ket{000},\ket{111}}$. In quantum repetition code for bit-flips we presented an ad-hoc encoding circuit for this code as
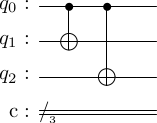
We will see later on how to construct this systematically.
Syndrome measurements: We saw in syndrome measurements for stabilizer codes this is achieved using the following circuit.
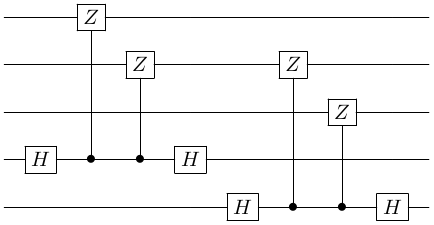
Here we are measuring the two generators $P_1$ and $P_2$.
Decoding: In quantum repetition code for bit-flips we noted that the encoding circuit for the repetition code is self-inverse, and can also be used for decoding. We will present a different procedure later on.
Task 1 (On paper)#
Show that the repetition code for phase-flips is also a stabilizer code.
Which errors are correctable by a stabilizer code#
Up till now, we have discussed three codes, and discovered that they all correct different sets of errors
- The repetition code for bit-flips corrects all single-qubit $X$ errors.
- The repetition code for phase-flips corrects all single-qubit $Z$ errors.
- The Shor code corrects all single-qubit errors.
Is there a rule that tells us which errors are correctable by the code? Indeed there is.
Theorem: Let $S$ be a stabilizer group, with generators $\set{g_i}$, and let $C(S)$ be the associated stabilizer code. Then $C(S)$ detects an error $E \in \st{P}_n$ if it anti-commutes with at least one generator $g_k$ of $S$.
Let's explore why this theorem is correct. To detect errors, we measure all the generators of the stabilizer group. Let's concentrate on the measurement of just one generator $g_k$. There are three possibilities.
- No error has occured and the data qubits are in state $\ket{\bar\psi}$.
- Error $E$ has occured, and the data qubits are in state $E\ket{\bar\psi}$. The two sub-possibilities are
- (a) $E$ commutes with $g_k$.
- (b) $E$ anti-commutes with $g_k$.
Let's analyze each possibility one by one. We will need to recall from syndrome measurements, an alternate view that if we measure $g_k$ on some state $\ket{\phi}$, then at the end of the measurement circuit, the qubits will be in state \begin{equation} \ket{\Phi} = (\ket{\phi} + g_k\ket{\phi})\ket{0} + (\ket{\phi} - g_k\ket{\phi})\ket{1}, \end{equation} where as per the possibilities above either $\ket{\phi}$ is the uncorrupted state $\ket{\bar\psi}$ or the corrupted state $E\ket{\bar\psi}\}$.
Possibility 1: no error.#
If there is no error, then $\ket{\phi} = \ket{\bar\psi}$ and so $\ket{\Phi} = \ket{\bar\psi}\ket{0}$. Consequently measuring the ancilla will yield 0.
Possibility 2 (a) $E$ commutes with $g_k$#
Now, $\ket{\phi} = E\ket{\bar\psi}$. First note that \begin{equation} g\ket{\phi} = g(E\ket{\bar\psi}) = Eg\ket{\bar\psi} = E\ket{\bar\psi} = \ket{\phi}. \end{equation} Hence, $\ket{\Phi} = \ket{\phi}\ket{0}$. Again, we discover that the ancilla will measure 0.
Possibility 2 (b) $E$ anti-commutes with $g_k$#
Now, $\ket{\phi} = E\ket{\bar\psi}$. First note that \begin{equation} g\ket{\phi} = g(E\ket{\bar\psi}) = -Eg\ket{\bar\psi} = -(E\ket{\bar\psi}) = -\ket{\phi}. \end{equation} Hence, $\ket{\Phi} = \ket{\phi}\ket{1}$. This time, the ancilla will measure 1.
What we have discovered is that only if and only if $E$ and $g_k$ anti-commute does the ancilla trigger. Therefore, it is quite easy to see that if at least one of $E$ and $\set{g_i}$ anti-commute, the code will detect the error.
A fourth possibility#
Note, that any code is also immune to errors that don't change the state. For instance, for the Shor code, we saw that errors like $Z_0Z_1$ leave $\ket{\bar\psi}$ unchanged.
Task 2 (On paper)#
Determine the commutation relations of single-qubit $X$ errors with the generators of the repetition code for bit-flips. Put 0 in the table if they commute, and 1 if they anti-commute.
| Error \ Generator | $Z \otimes Z \otimes I$ | $Z \otimes I \otimes Z$ |
|---|---|---|
| $I \otimes I \otimes I$ | ||
| $X \otimes I \otimes I$ | ||
| $I \otimes X \otimes I$ | ||
| $I \otimes I \otimes X$ |
Compare with the syndrome table that we presented in quantum repetition code for bit-flips.
Task 3 (On paper)#
Determine the commutation relations of single-qubit $Z$ errors with the generators of the repetition code for phase-flips. Put 0 in the table if they commute, and 1 if they anti-commute.
| Error \ Generator | $X \otimes X \otimes I$ | $X \otimes I \otimes X$ |
|---|---|---|
| $I \otimes I \otimes I$ | ||
| $Z \otimes I \otimes I$ | ||
| $I \otimes Z \otimes I$ | ||
| $I \otimes I \otimes Z$ |
Compare with the syndrome table that we presented in quantum repetition code for phase-flips
One important lesson you can take away from the above is that to detect $X$ type errors, we need $Z$ type generators. And to detect $Z$-type errors, we need $X$-type generators. This observation will be useful, when we construct more stabilizer codes.
Size of a stabilizer code#
Recall the sizes of the codes we have seen
| Code | No. of logical bits/qubits | No. of physical bits/qubits |
|---|---|---|
| classical repetition code | 1 | 3 |
| Hamming code | 4 | 7 |
| quantum repetition codes | 1 | 3 |
| Shor code | 1 | 9 |
If we define a stabilizer code $C(S)$ using some stabilizer group $S$, how many logical qubits are encoded into how many physical qubits? For this the rules are as follows.
- If $S$ is a subgroup of $\group{P}_n$, then $C(S)$ has $n$ physical qubits.
- If $S$ has $m$ generators, then $C(S)$ has $k=n-m$ logical qubits.
These three quantities $n,m,k$ will be very important in our further analysis.
Distance of a stabilizer code#
The distance of the code determines how many errors it can correct. A code with distance $d$ can correct $\lfloor (d-1)/2 \rfloor$ errors (the $\lfloor * \rfloor$ indicates the floor function).
The simplest way to find the distance is as follows.
The weight of a Pauli operator is the number of non-identity operators in it.
For instance, $X \otimes I \otimes Z \otimes I$ has a weight of two.
The distance of stabilizer code $C(S)$ is the minimum weight operator in $\group{P}_n$ that is not in $S$ but still commutes with all members of $S$.
Example: For the repetition code for bit-flips $S$ was generated by $P_1 = Z \otimes Z \otimes I$ and $P_2 = Z \otimes I \otimes Z$. Now, the operator $Q = Z \otimes I \otimes I$ commutes with both $P_1$ and $P_2$ but is not in $S$. $Q$ has weight 1, so the code has distance $d=1$.
Since $\lfloor (1-1)/2 \rfloor = 0$, this indicates that there are one qubit errors that the repetition code cannot correct. Obviously, these are the single-qubit phase errors.
Labeling stabilizer codes#
A quantum code with distance $d$ is labelled as $[[n,k,d]]$. The double brackets remind us that it is a quantum code.