The Anti-Infinity Parade

Logical Operations for the Steane Code

Today, I want to discuss how to obtain a universal set of gates for the Steane code.

Previously, we discussed Gottesman's method for constructing the encoded $\bar{X}$ and $\bar{Z}$ logical operations for stabilizer codes.

import stac
cd = stac.CommonCodes.generate_code('[[7,1,3]]')
cd.construct_logical_operators()
print('encoded X =')
stac.print_paulis(cd.logical_xs)
print('encoded Z =')
stac.print_paulis(cd.logical_zs)

encoded X =

$\displaystyle IIIIXXX$

encoded Z =

$\displaystyle ZZIIIIZ$

There are many other $7$-qubit Pauli operators that can act as $\bar{X}$ and $\bar{Z}$. A nicer choice is $$\bar{X} = X_0X_1X_2X_3X_4X_5X_6,$$ $$\bar{Z} = Z_0Z_1Z_2Z_3Z_4Z_5Z_6.$$

Clifford gates

Recall that the Clifford group is generated from the operations $H, S, CX$. We will first show how to find the logical

Hadamard gate

The Hadamard gate is also transversal (no two qubit gate between the qubits of a single block). It is $$\bar{H} = \otimes_{i=0}^6 H_i = H_0H_1H_2H_3H_4H_5H_6.$$ Why do we know this works? We can check that $\bar{H}\bar{X}\bar{H}^\dagger = \bar{Z}$, and that $\bar{H}\bar{Z}\bar{H}^\dagger = \bar{X}$, which are the required relations that $\bar{H}$ must obey.

logicalH = stac.Circuit()
for i in range(7):
    logicalH.append('H', i)
logicalH.draw(output='latex',scale=0.7)

$CX$ gate

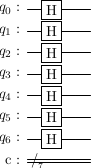
The $CX$ gate is also transversal and actually just made of seven $CX$ gates. Let us have two logical qubits, and designate one as control and the other as target. Let the physical qubits of the control logical qubits be indexed by $(c,i)$ and those of the target logical qubit be indexed by $(t,i)$. Then $$\bar{CX}_{c,t} = \otimes_{i=0}^6 CX_{(c,i),(t,i)}.$$

To check that this works, we have to verify the conjgation relations that we had previously.

Exercise: check that the $\bar{CX}$ satisfies these conjugation relations.

logicalCX = stac.Circuit()
for i in range(7):
    logicalCX.append('CX', i,7+i)
logicalCX.draw(output='latex',scale=0.7)

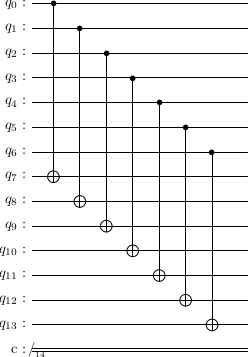
Logical $S$ gate

The $S$ gate is the gate, $$S = \begin{pmatrix}1 & 0 \\ 0 & \iu\end{pmatrix},$$ but is often defined in a nicer fashion with an overall phase factor as $$S = \begin{pmatrix}e^{-\iu\frac{\pi}{4}} & 0 \\ 0 & e^{\iu\frac{\pi}{4}}\end{pmatrix}.$$

Exercise: Compute the conjugacy relations of $S$ i.e. $SGS^\dagger$ for $G=X,Y$.

Let $$\bar{S} = \otimes_{i=0}^6 ZS.$$

Exercise: Verify that the defined $\bar{S}$ satisfies the conjugacy relations that $S$ should have.

The $T$ gate

The Clifford gate set does not allow us to do universal quantum computation, but the addition of the $T$ gate will. The $T$ gate is $$S = \begin{pmatrix}1 & 0 \\ 0 & e^{i\frac{\pi}{4}}\end{pmatrix},$$ or $$S = \begin{pmatrix}e^{-\iu\frac{\pi}{8}} & 0 \\ 0 & e^{-\iu\frac{\pi}{8}}\end{pmatrix}.$$

Magic states

For the Steane code, it's not possible to create a transversal $T$ gate on an encoded qubit. The way to obtain the $T$ gate is via magic states. The relevant magic state in our case is $$\ket{T} = T\ket{+} = \frac{\ket{0} + e^{i\frac{\pi}{4}}\ket{1}}{\sqrt{2}}.$$ This state is used in the following circuit, where $\ket{\psi}=\alpha\ket{0} + \beta\ket{1}$ be some unknown state on which we want to apply the $T$ gate, i.e we want $T\ket{\psi} = \alpha\ket{0} + \beta e^{i\frac{\pi}{4}}\ket{1}$.

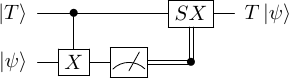
Let's evaluate to make sure everything works. Starting with $\ket{T}\ket{\psi}$, if we apply the $CX$ gate from the first qubit to the second, we obtain, $$CX_{01}\ket{T}\ket{\psi} = CX_{01}(\ket{0}+e^{i\frac{\pi}{4}}\ket{1})(\alpha\ket{0}+\beta\ket{1})/\sqrt{2},$$ $$= (\alpha\ket{00} + \beta\ket{01} + \alpha e^{i\frac{\pi}{4}}\ket{11} + \beta e^{i\frac{\pi}{4}}\ket{10})/\sqrt{2},$$ $$= \frac{1}{\sqrt{2}}(\alpha\ket{0} + e^{i\frac{\pi}{4}}\beta\ket{1})\ket{0} + \frac{1}{\sqrt{2}}(\beta\ket{0} + e^{i\frac{\pi}{4}}\alpha\ket{1})\ket{1}.$$ Next, we measure the second qubit in the $Z$ basis. We either obtain $0$ and the first qubit is left in the state $$\alpha\ket{0} + \beta e^{i\frac{\pi}{4}}\ket{1} = T\ket{\psi},$$ or we obtain $1$ and the first qubit is left in the state $$\beta\ket{0} + \alpha e^{i\frac{\pi}{4}}\ket{1}.$$ In the first case, we have obtained the desired state. In the second case, if we just apply, $SX$ to the state, we obtain $T\ket{\psi}$.

In summary, if it is possible to create a $\ket{T}$ state, one can apply a $T$ gate to any state using just Clifford operations.

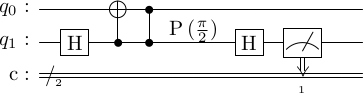
Creating the $\ket{T}$ state

One can probabilistically create the $\ket{T}$ state. The circuit for it is given below, where the second control gate is a $CS$ gate.

Tstateprep = stac.Circuit()
Tstateprep.append('H', 1)
Tstateprep.append('CX', 1, 0)
Tstateprep.append('cp(pi/2)', 1, 0)
Tstateprep.append('H', 1)
Tstateprep.append('M', 1)
Tstateprep.draw()
# an iteration that yielded 0 for the measurement
Tstateprep.simulate()

  basis  amplitude
-------  -----------
     00   0.707
     10  0.707j

# an iteration that yielded 1 for the measurement
Tstateprep.simulate()

  basis  amplitude
-------  -----------
     01   0.707
     11  -0.707j

Exercise: Evaluate this circuit by hand to show that if the measurement outcome is $0$, then the first qubit will be in the $\ket{T}$ state.

If instead the measurement outcome is $1$, then we apply the $Z$ operator to correct the state.