The Anti-Infinity Parade

An introduction to the Steane code

The Steane code is a simple quantum error correction code, that nevertheless has a number of interesting properties.

• The Steane code encodes the state of one logical qubit into the state of 7 physical qubits, in a way that any one qubit error can be corrected.
• By concatenating the code with itself, more errors can be corrected.
• Most gates and operations that we would like to do can be done in fault-tolerant fashion.
• It is a stabilizer code, as well as a CSS code. This is useful because such codes have a well-developed mathematical machinery.

While, it will likely never be used for actual quantum computation, it is a good test bed for both learning about quantum error correction, and possibly to run experiments on NISQ devices. The

Hamming Code

The Steane code is related to the classical error-correcting code, the Hamming code [1]. In the Hamming code, a message $m$ of 4 bits is encoded into a block $c=mG$ of 7 bits, where the generator matrix $$G=\begin{pmatrix} 0 & 1 & 0 & 1 & 0 & 1 & 0 \\ 0 & 0 & 1 & 1 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 1 & 1 & 1 \\ 1 & 0 & 0 & 1 & 0 & 1 & 1 \\ \end{pmatrix}.$$ There are $2^4=16$ possible messages, and associated codewords. The codewords have the property that they obey the relation $Hc = 0$, where the parity check matrix $$H=\begin{pmatrix} 1 & 1 & 1 & 1 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 0 & 1 & 0 & 1 \\ \end{pmatrix}.$$ The fact that $Hc=0$ for all valid codewords can be used to detect and correct errors. Suppose some error occurs and flips some bits of $c$. This operation can be represented as $c+e$, where $e$ is another 7 bit vector. Applying $H$ to the corrupted codeword $c+e$, we obtain the syndrome $H(c+e) = He$, which is a length 3 vector. Each entry is a linear combination of the entries of the corrupted codeword, and acts as a check. In particular, there are 8 possible errors that this code can correct - no error, or a single bit-flip on one of the bits. If there is no error, then $He=0$. Otherwise, as each column of $H$ is unique, an $e$ with exactly one 1 will be equal to exactly one of these columns. Hence, we can match $He$ with the columns of $H$ to determine which bit has flipped. Finally we can correct $c+e$ by adding $e$ to it.

One important fact to note about the above is that the operation $H(c+e)=He$ reveals no information about $c$, but only about $e$. While not so important for classical error correction, this feature is required for every quantum error correcting code.

Stabilizer codes

A quantum error correcting code has to protect against not just flip errors, but also phase errors, i.e. the state $\ket{\psi} = \alpha\ket{0} + \beta\ket{1}$ can be transformed to $X\ket{\psi} = \alpha\ket{1} + \beta\ket{0}$ or $Z\ket{\psi} = \alpha\ket{0} - \beta\ket{1}$, or both. Stabilizer codes do so by encoding the quantum state $\ket{\psi}_k$ into a state $\ket{\bar\psi}_n$ stabilized by an appropriate Abelian subgroup $S$ of the Pauli group $\mathcal{P}_n$. This means for every $s \in S$, the encoded state $\ket{\bar\psi}_n$ is a $+1$ eigenvalue state. We can write this as $$s\ket{\bar\psi}_n = \ket{\bar\psi}_n, \quad \forall s \in S.$$

Any group can be specified by a set of generators, and such a description is efficient. If a group is Abelian, as is $S$, then $\log_2|S|$ generators are sufficient to describe the group. Moreover, we note that for a stabilizer group $S$, if its generators $\{ g_i \}$ stabilize $\ket{\bar\psi}$ then so do all members. And if any $s \in S$ does not stabilize a state, then at least one generator will not as well. Hence, we can almost entirely work with generators when talking about stabilizer groups and codes.

A given group/code $S$ can correct against a specific set of of errors $\mathcal{E} = \{E_i\}$, and their linear combinations. The action of any non-trivial error in $\mathcal{E}$ is that $E\ket{\bar\psi}$ is no longer stabilized by at least one generator. Hence, to detect errors, we have to check via appropriate measurements which, if any, of the stabilizers don't stabilize a state.

To compute which errors lead to which generator not being stabilized, the rule is that if and only $E$ and $g_i$ don't commute will the corrupted state not be stabilized by $g_i$. To make computation easy, here is a simple rule. Let any operator $A$ in $\mathcal{P}_n$ be associated with a binary vector of length $2n$. This vector has form $v = (a|b)$ where $a$ is the "$X$ part" and and $b$ is the "$Z$ part". Let $A = \prod_i P_i$, where $P_i \in \{I_i, X_i, Y_i, Z_i\}$. Then, $$a_i = 0, b_i = 0 \text{ if } P_i = I_i$$ $$a_i = 1, b_i = 0 \text{ if } P_i = X_i$$ $$a_i = 1, b_i = 1 \text{ if } P_i = Y_i$$ $$a_i = 0, b_i = 1 \text{ if } P_i = Z_i$$ For example if $n=4$, then $X_0I_1Z_2Y_3$ is associated with the vector $v=(1 0 0 1|0 0 1 1)$.

Then $E \sim (a|b)$ and $g_i \sim (c|d)$ anti-commute iff $g_i\cdot E = a\cdot d + b\cdot c = 1$, and commute iff $g_i\cdot E = 0$.

CSS codes

CSS codes are those stabilizer codes, where each generator $g_i$ of $S$ either consists of a product of $X$ operators, or a product of $Z$ operators. A very simple CSS code is the repetition code, in which a one qubit state is encoded into a three qubit state, and that can corrects a single bit-flip error on any of the three qubits. The code has the corresponding stabilizer group $S = \langle Z_1 Z_2, Z_2Z_3\rangle$. You can see that every generator is only a product of $Z$ operators, so this is a CSS code. We will note the design principle of quantum error correction: a $Z$-type generator fails to stabilize a state that has encounted some $X$ error. Here if error $X_1$ occurs, then the first stabilizer will fail to stabilize the corrupted state, etc.

Similarly, another design principle is that $X$-type generators will fail to stabilize a state that has encounted a $Z$ error. This is why the repetition code that corrects a single phase-flip error is associated with the group $S = \langle X_1 X_2, X_2X_3\rangle$.

Steane Code

Keeping the above in mind let us now present the Steane code. We are going to encode the state of one qubit into the state of seven qubits. Let's try to design it, using the fact that it is associated with the Hamming code.

First, we need to correct a phase-flip error on any of the seven qubits. There are eight total possibilities here: no phase-flip error, or a phase-flip error on a single qubit. To distinguish between these eight possibilities, we need 3 bits of information. A measurement of a generator can yield one bit of information (either it stabilizes the corrupted state or not). So, we need three $X$-type generators to determine this. For our case, we are going to use the Hamming code to do this. Each row of the parity check matrix, $$H=\begin{pmatrix} 1 & 1 & 1 & 1 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 0 & 1 & 0 & 1 \\ \end{pmatrix},$$ of the Hamming code (which were the checks in the classical case), will define one generator for our code. Each row defines the $X$-part of the length $2n$ vector associated with each generator (and the $Z$-part is zero). Reading off, the generators are $$g_0 = X_0X_1X_2X_3$$ $$g_1 = X_0X_1X_4X_5$$ $$g_2 = X_0X_2X_4X_6$$ Why does this work? Or to ask differently, can we say without doing any calculations involving quantum states or operators, that for each of the 8 possible errors at least one of the generators will trigger? Moreover, will for each of the 8 possible errors a unique set of generators will trigger? The answer to this question is that we already know that in the classical case, each of the 8 errors result in a different syndrome, and the same thing will happen in the quantum case. Why is this? Because if $g_i \sim (c|0)$ and the error $E \sim (0|b)$, where $b$ has exactly one non-zero entry (corresponding to the single-qubit phase-error), then the commutation relations, $\{g_i\cdot E = c\cdot b\}_i$ can just be written as $Hb$. This is exactly like the classical syndrome calculation, which we already know yields exactly enough information to determine the error.

Great! Now, what about the bit-flip errors. Well, we will need $Z$ type errors, and we will construct them from $H$ in exactly the same way. We will have, $$g_3 = Z_0Z_1Z_2Z_3$$ $$g_4 = Z_0Z_1Z_4Z_5$$ $$g_5 = Z_0Z_2Z_4Z_6$$ Measuring these on the corrupted codewords will yield information about any bit-flip errors.

Usually, all the generators are written as one matrix, with one row for each generator. For the Steane code, the matrix is $$H = \left(\begin{array}{ccccccc|ccccccc} 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & 0 & 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 \\ \end{array}\right).$$

Encoded zero state

To be able to see the code in action, we should construct the encoded basis states $\{\ket{\bar 0}, \ket{\bar 1}\}.$ Like all encoded states, these states are stabilized by all elements of the stabilizer group, i.e. $$\forall s\in S \quad s\ket{\bar 0} = \ket{\bar 0},$$ and similarly for $\ket{\bar 1}$.

We use this property to construct the zero state. More correctly, we will construct one state that is in the code, and designate it as the zero state. To do so, consider the action of, say $g_0$ on $\ket{0000000}$. We see that $$g_0\ket{0000000} = \ket{1111000}.$$ This tell us that $\ket{0000000}$ is not stabilized by $g_0$. But, note that $$g_0\ket{1111000} = \ket{0000000}.$$ So $g_0$ converts between these two states. This tell us that the state $\ket{0000000} + \ket{1111000}$ is stabilized by $g_0$ (we are going to ignore normalization). Further note that $$(I + g_0)\ket{0000000} = \ket{0000000} + \ket{1111000}.$$ If you think about it a moment, you will realize that $I + g_0$ acting on any state, constructs a state stabilized by $g_0$.

With this in mind, we see that $$(I + g_1)(I + g_0)\ket{0000000} = (I+g_1)\ket{0000000} + (I+g_1)\ket{1111000}$$ is stabilized by both $g_0$ and $g_1$. Taking the same argument forward, we determine that $$\ket{\phi} = (I+g_2)(I + g_1)(I + g_0)\ket{0000000}$$ $$= \ket{0000000} + \ket{1100110}+ \ket{1111000} + \ket{0011110}$$ $$+ \ket{1010101} + \ket{0110011}+ \ket{0101101} + \ket{1001011}.$$

Now, we could blindly compute the action of $I+g_i$ on this state for the $Z$-type generators, but instead we think about it for a second. First realize that the rows of the parity-check matrix must be linearly independent (so they generate independent checks), and this means that every pair coincides at exactly an even number of location. This means that in $g_i\ket{\phi}$ for $i=3,4,5$, there will be an even number of $Z$ operators coinciding with the $1$s in each component state. For instance, note that $Z_0Z_1Z_2Z_3\ket{0011110} = \ket{0011110}$ because of this even coincidence. Hence, the state $\ket{\phi}$ is already stabilized by $g_3,g_4,g_5$. Consequently, we can arbitrarily start calling $\ket{\phi} = \ket{\bar 0}$ the zero state.

In order to construct the $\ket{\bar 1}$ state, the easiest way is by using the encoded gate operations.

Encoded Pauli gate operations

The logical single-qubit operations, $\bar{X}, \bar{Z}$ are quite simple to construct. They are $$\bar{X} = X_0X_1X_2X_3X_4X_5X_6$$ $$\bar{Z} = Z_0Z_1Z_2Z_3Z_4Z_5Z_6$$

One can check that these anti-commute $\{\bar{X}, \bar{Z}\} = 0$. They also commute with every element in Steane code's stabilizer group, but are not in the group itself. Which means that they preserve the codespace but do rotate it.

Clifford gates

The Clifford gates are generated by $\{H, S, CX\}$, and these gates, along with the Pauli gates, are all we need for correcting errors on the physical qubits. The logical $H$ and $S$ gates are obtained in a transversal fashion, $$\bar{H} = H_0H_1H_2H_3H_4H_5H_6$$ $$\bar{S} = S_0S_1S_2S_3S_4S_5S_6$$ We can check this is correct by verifying their conjugation relations with the Pauli gates.

For the logical $CX$ gate, we need two logical qubits. Suppose, the first logical qubit is encoded in physical qubits 0-6, and the second logical qubit in physical qubits 7-13. Then, the logical $CX$ with the first logical qubit as control is as follows.

# https://github.com/abdullahkhalids/stac
import stac
cx_circuit = []
for i in range(7):
    cx_circuit.append(['cx', i, 7+i])

stac.draw_circuit(cx_circuit, output='latex', scale=0.7)

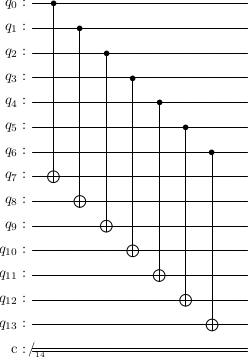
Transversality and Fault-Tolerance

One important aspect of the gates discussed above are that they are transversal. To understand this, we will call the qubits that make up one logical qubits, or a set of ancilla brought about to do a single measurement, a code block. Then a transversal operation is one which (1) applies one qubit gates to the qubits in a code block, and (2) only interacts each qubit in a given block with at most one unique qubit in a different code block. You can see that the Clifford gates for the Steane code are all transversal.

This is important for fault tolerance. What is that? A fault-tolerant quantum circuit is one in which, if an error occurs on a single qubit, it doesn't produce more errors in the same block. This ensures our model of errors where we say that all errors occur independently. If an error in a block led to more errors in the same block, those would be correlated errors. Such errors would make it much more difficult to do error-free logical computation.

Encoded one state

The encoded one state is simply $$\bar{X}\ket{\bar 0} = \ket{1111111} + \ket{0011001} + \ket{0000111} + \ket{1100001}$$ $$+ \ket{0101010} + \ket{1001100} + \ket{1010010} + \ket{0110100}$$

Tomorrow we will start constructing and simulating various circuits related to the Steane code.

[1] J. Preskill, Fault-Tolerant Quantum Computation, (1997).